Pengertian Dan Sifat Layang-Layang Serta Rumus Luas Dan Keliling Layang-Layang Dilengkapi Dengan Teladan Soalnya

Berikut ini merupakan pembahasan pengertian layang layang, sifat layang layang, rumus luas layang layang, rumus keliling layang layang, teladan soal layang layang, teladan soal keliling layang layang, teladan soal luas layang layang.

Pengertian Layang-layang

Layang-layang merupakan salah satu berdiri segi empat sebagaimana bangun-bangun segi empat lainnya seperti; persegi, persegi panjang, belah ketupat, jajar genjang, trapesium dan lain-lain.

Apakah yang dimaksud dengan layang-layang? Apa pengertian layang-layang?

Layang-layang adalah berdiri datar dua dimensi yang dibuat oleh dua pasang rusuk yang masing-masing pasangannya sama panjang dan saling membentuk sudut.

Sifat-Sifat Layang-Layang

Gambar (a) dan (b) di bawah ini mengatakan dua segitiga sama kaki dengan panjang ganjal sama, tetapi panjang sisi antara kedua segitiga itu tidak sama.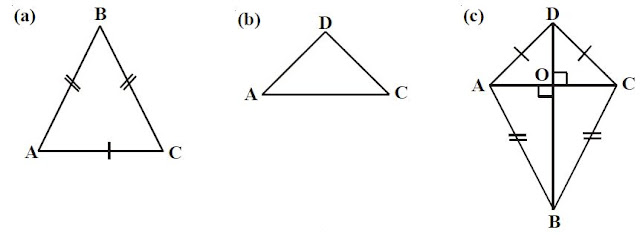

Berikut ini merupakan pembahasan pengertian layang layang Pengertian dan Sifat Layang-layang serta Rumus Luas dan Keliling Layang-layang Dilengkapi dengan Contoh Soalnya

Gambar: Model Layang-layang

Jika kedua segitiga itu diimpitkan pada alasnya, maka akan diperoleh berdiri segi empat ABCD menyerupai Gambar c. Bangun ini disebut layang-layang.

Perhatikan kembali Gambar c, pada gambar terlihat:

a. AD = CD dan AB = BC (sisinya sepasang-sepasang sama panjang).

b. ÐBAO = ÐBCO dan ÐDAO = ÐDCO , sehingga ÐBAD = ÐBCD. Layang-layang mempunyai sepasang sudut berhadapan yang sama besar.

c. ÐABO = ÐCBO dan ÐADO = ÐCDO. Masing-masing sudut dibagi oleh diagonal BD . Diagonal BD merupakan sumbu simetri.

d. DO dan BO merupakan garis berat DACD dan DACB, maka AO = CO dan BD ^ AC

Jika salah satu diagonal membagi dua sama panjang diagonal yang lain, maka kedua diagonal itu saling tegak lurus.

Dari uraian di atas sanggup disimpulkan bahwa sifat-sifat layang-layang:

a. sisinya sepasang-sepasang sama panjang

b. sepasang sudut yang berhadapan sama panjang

c. salah satu diagona membagi dua sama panjang diagonal lainnya, maka kedua diagona tersebut saling tegak lurus.

Rumus Keliling Layang-Layang

Keliling layang-layang sama halnya dengan keliling segi empat lainnya, yaitu jumlah keempat sisinya. Perhatikan gambar layang-layang di bawah ini.

Gambar: Layang-layang ABCD

Keliling layang-layang ABCD yaitu AB + BC + CD + DA

Karena AB = BC dan AD = CD , maka keliling layang-layang ABCD = 2(AB + CD)

Contoh Soal Keliling Layang-layang

Diketahui layang-layang PQRS (lihat gambar di bawah ini). Kelilingnya 40 cm dan PQ = 12 cm. Tentukan panjang sisi yang lain.

Gambar: Layang-layang PQRS

Penyelesaian:
PQ = 12 cm, QR = PQ, QR = 12 cm

Keliling = 2(PQ + PS)
2(12 + PS) = 40
24 + 2PS = 40
2PS = 40 – 24
= 16
PS = 16:2
= 8
Kaprikornus panjang PQ = QR = 12 cm dan panjang PS = RS = 8 cm

Rumus Luas Daerah Layang-Layang

Gambar di bawah ini mengatakan layang-layang PQRS dengan diagonal PR = QS saling berpotongan tegak lurs di titik T.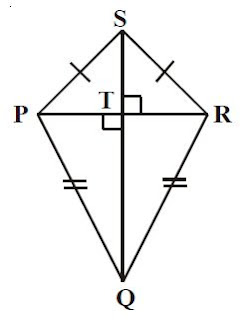

Gambar: Layang-layang PQRS

Luas PQRS = luas PQR + luas PRS
= ½PR x QT + ½PR x ST
= ½PR (QT + ST )
= ½PR x QS
Kaprikornus luas layang-layang PQRS = ½PR x QS

Keliling layang-layang ABCD = AB + BC + CD + DA
= 2 x (AB + AD)
Luas layang-layang

Luas layang-layang sama dengan setengah hasil kali diagonal-diagonalnya. Misalnya luas yaitu L dan diagonal-diagonalnya d1 dan d2, maka L = ½ x d1 x d2

Contoh Soal Luas Layang-layang

Suatu layang-layang, panjang diagonalnya masing-masing 40 cm dan 18 cm. Hitunglah luas layang-layang tersebut.

Penyelesaian:
Misalkan luas layang-layang = L cm2
Diagonal-diagonalnya d1 = 40 cm dan d2 = 18 cm
L = ½ x d1 x d2
= ½ x 40 x 18
= 360
Jadi, luas layang-layang yaitu 360 cm².

Baca juga: Sifat-sifat Belah Ketupat

Sumber https://www.berpendidikan.com