Cara Memilih Himpunan Penyelesaian Sistem Persamaan Linear Dua Variabel (Spldv) Dengan Metode Grafik, Subsitusi Dan Eliminasi
Berikut ini merupakan pembahasan perihal Sistem Persamaan Linear Dua Variabel yang mencakup sistem persamaan linear dua variabel, spldv, menyelesaiakan sistem persamaan linear dua variabel dengan grafik, persamaan linear dua variabel metode grafik, subsitusi, eliminasi dan campuran.
Apabila terdapat dua buah persamaan linear dua variabel yang berbentuk ax + by = c dan px + qy = r, dimana persamaan yang satu dan lainnya tidak terpisahkan, maka persamaan-persamaan tersebut dinamakan sistem persamaan linear dua variabel.
Bentuk umum sistem persamaan linear dua variabel adalah:
ax + by = c
px + qy = r
Dalam sistem persamaan linear dua variabel (SPLDV) di atas, a, b, p, dan q disebut koefisien, x dan y ialah variabel dari SPLDV, serta c dan r disebut konstanta.
Nilai x dan y yang memenuhi kedua persamaan tersebut dinamakan penyelesaian sistem persamaan linear dua variabel. Semua variabel, koefisien dan konstanta dalam SPLDV merupakan bilangan real.
Pertanyaan kita kini ialah bagaimana cara untuk memilih himpunan penyelesaian dari sistem persamaan linear dua variabel?
Jika garisnya tidak berpotongan atau sejajar maka himpunan penyelesaiannya ialah himpunan kosong. Namun demikian, jikalau garisnya berhimpit maka jumlah himpunan penyelesaiannya tak berhingga.
Titik potong kedua garis ialah (2, 2). Makara himpunan penyelesaian dari sistem persamaan tersebut ialah (2, 2).
2. Tentukan himpunan penyelesaian dari sistem persamaan x – y = 2 dan 2x – 2y = –4 dengan memakai metode grafik! (x dan y himpunan bilangan real)
Kedua garis ternyata sejajar, sehingga tidak ada titik potong. Makara himpunan penyelesaiannya ialah himpunan kosong { }.
3. Tentukan himpunan penyelesaian dari sistem persamaan x – y = –2 dan 2x – 2y = –4 dengan memakai metode grafik! (x dan y himpunan bilangan real)
Penyelesaian:
Kedua garis ternyata berimpit. Maka himpunan penyelesaian dari sistem persamaan linear dua variabel tersebut tak berhingga banyaknya.
Langkah-langkah pengerjaan dengan memakai metode substitusi untuk mencari himpunan penyelesaian dari SPLDV ialah sebagai berikut.
Penyelesaian:
Langkah 1 (mengubah ke dalam bentuk x = ... atau y = ...)
Langkah 2 (substitusi y = 4 – 2x ke persamaan –x + 2y = –7)
Langkah 3 (substitusi x = 3 ke 2x + y = 4 atau –x + 2y = –7)
Jadi, himpunan penyelesaian dari sistem persamaan 2x + y = 4; x,y Î R dan –x + 2y = 7; x, y Î R ialah {(3, -2)}.
Caranya dengan menjumlahkan atau mengurangkan kedua sistem persamaan tersebut. Untuk memilih variabel y, maka hilangkan terlebih dahulu variabel x. Begitu pula sebaliknya, untuk memilih variabel x, maka hilangkan terlebih dahulu variabel y.
Sebagai catatan, untuk menghilangkan variabel x atau y maka koefisien dari masing-masing variabel dalam sistem persamaan haruslah sama.
Jika salah satunya tidak sama maka harus disamakan dahulu. Caranya mengalikan dengan bilangan bundar tertentu sehingga koefisiennya menjadi sama. Perhatikan pola berikut!
Penyelesaian:
• Mengeliminasi variabel x (untuk mencari y)
• Mengeliminasi variabel y (untuk mencari x)
Jadi, himpunan penyelesaian dari sistem persamaan tersebut ialah {(0, 2)}.
Oleh alasannya itu, kita sanggup memakai metode campuran, yaitu memilih salah satu variabel x atau y dengan memakai metode eliminasi.
Hasil yang diperoleh dari x atau y lalu disubstitusikan ke salah satu persamaan linear dua variabel tersebut. Perhatikan pola berikut ini!
Penyelesaian:
• Mengeliminasi variabel x (untuk mencari y)
• Substitusi y = 4 ke persamaan 2x + 3y = 10
Jadi, himpunan penyelesaian dari sistem persamaan tersebut ialah {(-1, 4)}.
Baca juga: Soal Cerita Persamaan Linear Sumber https://www.berpendidikan.com
Sistem Persamaan Linear Dua Variabel
Dalam persamaan linear dua variabel kalian akan mene mukan himpunan penyelesaian yang berupa pasangan berurutan.Apabila terdapat dua buah persamaan linear dua variabel yang berbentuk ax + by = c dan px + qy = r, dimana persamaan yang satu dan lainnya tidak terpisahkan, maka persamaan-persamaan tersebut dinamakan sistem persamaan linear dua variabel.
Bentuk umum sistem persamaan linear dua variabel adalah:
ax + by = c
px + qy = r
Dalam sistem persamaan linear dua variabel (SPLDV) di atas, a, b, p, dan q disebut koefisien, x dan y ialah variabel dari SPLDV, serta c dan r disebut konstanta.
Nilai x dan y yang memenuhi kedua persamaan tersebut dinamakan penyelesaian sistem persamaan linear dua variabel. Semua variabel, koefisien dan konstanta dalam SPLDV merupakan bilangan real.
Pertanyaan kita kini ialah bagaimana cara untuk memilih himpunan penyelesaian dari sistem persamaan linear dua variabel?
Untuk memilih himpunan penyelesaian dari sistem persamaan linear dua variabel sanggup dilakukan dengan empat metode, yaitu metode grafik, metode substitusi, metode eliminasi, dan metode adonan (substitusi dan eliminasi).
1. Menentukan Himpunan Penyelesaian SPLDV dengan Metode Grafik
Ketika memakai metode grafik, kalian harus menggambar masing-masing persamaan linear dua variabel tersebut dalam koordinat kartesius. Himpunan penyelesaiannya ialah titik potong dari kedua garis.Jika garisnya tidak berpotongan atau sejajar maka himpunan penyelesaiannya ialah himpunan kosong. Namun demikian, jikalau garisnya berhimpit maka jumlah himpunan penyelesaiannya tak berhingga.
Contoh Soal dan Pembahasannya
1. Tentukan himpunan penyelesaian dari sistem persamaan 2x – y = 2 dan x + y = 4 dengan memakai metode grafik! (x dan y himpunan bilangan real)Titik potong kedua garis ialah (2, 2). Makara himpunan penyelesaian dari sistem persamaan tersebut ialah (2, 2).
2. Tentukan himpunan penyelesaian dari sistem persamaan x – y = 2 dan 2x – 2y = –4 dengan memakai metode grafik! (x dan y himpunan bilangan real)
Kedua garis ternyata sejajar, sehingga tidak ada titik potong. Makara himpunan penyelesaiannya ialah himpunan kosong { }.
3. Tentukan himpunan penyelesaian dari sistem persamaan x – y = –2 dan 2x – 2y = –4 dengan memakai metode grafik! (x dan y himpunan bilangan real)
Penyelesaian:
Kedua garis ternyata berimpit. Maka himpunan penyelesaian dari sistem persamaan linear dua variabel tersebut tak berhingga banyaknya.
2. Menentukan Himpunan Penyelesaian SPLDV dengan Metode Subtitusi
Setelah kita mencar ilmu cara memilih himpunan penyelesaian SPLDV memakai metode grafik, kini kita akan mempelajari cara memilih himpunan penyelesaian SPLDV memakai metode substitusi.Langkah-langkah pengerjaan dengan memakai metode substitusi untuk mencari himpunan penyelesaian dari SPLDV ialah sebagai berikut.
- Ubahlah salah satu persamaan ke dalam bentuk x = ... atau y = ...
- Masukkan (substitusi) nilai x atau y yang diperoleh ke dalam persamaan yang kedua
- Nilai x atau y yang diperoleh lalu disubstitusikan ke dalam salah satu persamaan untuk memperoleh nilai variabel lainnya yang belum diketahui (x atau y).
Contoh Soal dan Pembahasannya
Tentukan himpunan penyelesaian dari sistem persamaan 2x + y = 4; x,y Î R dan –x + 2y = –7; x,y Î R memakai metode substitusi!Penyelesaian:
Langkah 1 (mengubah ke dalam bentuk x = ... atau y = ...)
- 2x + y = 4
- y = 4 – 2x
Langkah 2 (substitusi y = 4 – 2x ke persamaan –x + 2y = –7)
- –x + 2y = –7
- –x + 2(4 – 2x) = –7
- –x + 8 – 4x = –7
- –x – 4x = –7 - 8
- –5x = –15
- x = –15:(–5)
- x = 3
Langkah 3 (substitusi x = 3 ke 2x + y = 4 atau –x + 2y = –7)
- 2x + y = 4
- 2(3) + y = 4
- 6 + y = 4
- y = 4 – 6
- y = –2
Jadi, himpunan penyelesaian dari sistem persamaan 2x + y = 4; x,y Î R dan –x + 2y = 7; x, y Î R ialah {(3, -2)}.
3. Menentukan Himpunan Penyelesaian SPLDV dengan Metode Eliminasi
Penyelesaian SPLDV dengan metode eliminasi intinya ialah menghilangkan (mengeliminasi) salah satu variabel dari sistem persamaan yang akan dicari himpunan penyelesaiannya.Caranya dengan menjumlahkan atau mengurangkan kedua sistem persamaan tersebut. Untuk memilih variabel y, maka hilangkan terlebih dahulu variabel x. Begitu pula sebaliknya, untuk memilih variabel x, maka hilangkan terlebih dahulu variabel y.
Sebagai catatan, untuk menghilangkan variabel x atau y maka koefisien dari masing-masing variabel dalam sistem persamaan haruslah sama.
Jika salah satunya tidak sama maka harus disamakan dahulu. Caranya mengalikan dengan bilangan bundar tertentu sehingga koefisiennya menjadi sama. Perhatikan pola berikut!
Contoh Soal dan Pembahasannya
Tentukan himpunan penyelesaian dari sistem persamaan 2x – y = –2; x,y Î R dan x + 2y = 4; x,y Î R dengan memakai metode elimi nasi!Penyelesaian:
• Mengeliminasi variabel x (untuk mencari y)
• Mengeliminasi variabel y (untuk mencari x)
Jadi, himpunan penyelesaian dari sistem persamaan tersebut ialah {(0, 2)}.
4. Menentukan Himpunan Penyelesaian SPLDV dengan Metode Campuran (Eliminasi dan Substitusi)
Dalam pengerjaan soal persamaan linear dua variabel, terkadang kita menemukan kesulitan jikalau memakai metoda eliminasi untuk memilih himpunan penyelesaiannya.Oleh alasannya itu, kita sanggup memakai metode campuran, yaitu memilih salah satu variabel x atau y dengan memakai metode eliminasi.
Hasil yang diperoleh dari x atau y lalu disubstitusikan ke salah satu persamaan linear dua variabel tersebut. Perhatikan pola berikut ini!
Contoh Soal dan Pembahasannya
Tentukan himpunan penyelesaian dari sistem persamaan x + 2y = 7; x,y∈R dan 2x + 3y = 10; x,y∈R memakai metode campur an!Penyelesaian:
• Mengeliminasi variabel x (untuk mencari y)
• Substitusi y = 4 ke persamaan 2x + 3y = 10
- 2x + 3y = 10
- 2x + 3(4) = 10
- 2x + 12 = 10
- 2x = –2
- x = –1
Jadi, himpunan penyelesaian dari sistem persamaan tersebut ialah {(-1, 4)}.
Baca juga: Soal Cerita Persamaan Linear Sumber https://www.berpendidikan.com





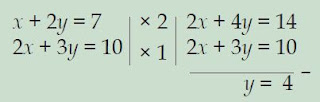
Post a Comment for "Cara Memilih Himpunan Penyelesaian Sistem Persamaan Linear Dua Variabel (Spldv) Dengan Metode Grafik, Subsitusi Dan Eliminasi"