Pengertian Peluang Suatu Kejadian, Frekuensi Relatif, Rumus Dan Pola Soal Peluang (Probabilitas)
Berikut ini yaitu pembahasan ihwal peluang yang mencakup pengertian peluang, pengertian kejadian, pengertian peluang suatu kejadian, Perhitungan Peluang Suatu Kejadian dengan Frekuensi Relatif, rumus peluang, kisaran nilai peluang, referensi soal peluang, pengertian probabilitas, rumus peluang matematika, peluang suatu kejadian, referensi soal probabilitas, pengertian frekuensi relatif.
Pada percobaan pelemparan sebuah dadu, ruang sampelnya yaitu S = {1, 2, 3, 4, 5, 6}, sedangkan titik-titik sampel percobaan tersebut yaitu 1, 2, 3, 4, 5, 6. Adapun sebarang himpunan penggalan dari ruang sampel disebut kejadian, biasanya dilambangkan dengan K. Misalnya, K = {2, 4, 6} yaitu tragedi munculnya muka dadu bertitik genap dengan n(K) = 3.
Ambillah sekeping uang logam, lalu lemparkan sebanyak 30 kali. Misalkan, hasil yang diperoleh yaitu muncul sisi gambar sebanyak 13 kali. Perbandingan banyak tragedi muncul sisi gambar dengan banyak pelemparan yaitu 13/30. Nilai inilah yang disebut frekuensi relatif.
a. Bertitik 1 sebanyak 25 kali.
b. Bertitik 3 sebanyak 17 kali.
c. Bertitik 6 sebanyak 56 kali.
Tentukan frekuensi relatif tragedi munculnya mata dadu bertitik 1, 3, dan 6.
Jawab:
Banyaknya percobaan yaitu 200
a. Kejadian munculnya muka dadu bertitik 1 sebanyak 25 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 1 yaitu 0,125.
b. Kejadian munculnya muka dadu bertitik 3 sebanyak 17 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 3 yaitu 0,085.
c. Kejadian munculnya muka dadu bertitik 6 sebanyak 56 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 6 yaitu 0,28.
Peluang munculnya setiap titik sampel di dalam ruang sampel yaitu sama, yaitu 1/6. Jadi, peluang munculnya muka dadu bertitik prima adalah
Selain dengan cara tersebut, nilai P(K) juga sanggup ditentukan dengan cara sebagai berikut.
S = {1, 2, 3, 4, 5, 6} maka n(S) = 6.
K = {2, 3, 5} maka n(K) = 3.
Uraian tersebut menjelaskan bahwa bila setiap titik sampel anggota ruang sampel S mempunyai peluang yang sama maka peluang tragedi K yang mempunyai anggota sebanyak n(K) dinyatakan sebagai berikut.
a. bertitik 3,
b. bertitik lebih dari tiga,
c. bertitik 1, 2, 3, 4, 5, 6,
d. bertitik lebih dari 6.
Jawab:
Oleh alasannya ruang sampelnya yaitu S = {1, 2, 3, 4, 5, 6} maka n(S) = 6.
a. Misalkan, A yaitu himpunan tragedi munculnya dadu bertitik 3 maka A = {3} sehingga n(A) = 1.
b. Misalkan, B yaitu himpunan tragedi munculnya dadu bertitik lebih dari 3 maka B = {4, 5, 6} sehingga n(B) = 3.
c. Misalkan, C yaitu himpunan tragedi munculnya mata dadu bertitik 1, 2, 3, 4, 5 dan 6 maka C = {1, 2, 3, 4, 5, 6} sehingga n(C) = 6.
Jadi, peluang munculnya mata dadu bertitik 1, 2, 3, 4, 5 dan 6 yaitu 1.
d. Misalkan, D yaitu himpunan tragedi munculnya mata dadu bertitik lebih dari 6 maka D = { } sehingga n(D) = 0.
Jadi, peluang munculnya mata dadu bertitik lebih dari 6 yaitu 0.
Pengertian Peluang Suatu Kejadian
Peluang atau kebolehjadian atau dikenal juga sebagai probabilitas adalah cara untuk mengungkapkan pengetahuan atau doktrin bahwa suatu tragedi akan berlaku atau telah terjadi. Konsep ini telah dirumuskan dengan lebih ketat dalam matematika, dan lalu dipakai secara lebih luas dalam tidak hanya dalam matematika atau statistika, tapi juga keuangan, sains dan filsafat.Peluang adalah impian terjadinya suatu tragedi yang dikuantitatifkan. Peluang bekerjasama dengan gagasan atau konsepkesempatan atau kemungkinan. Kita katakan peluangnya besar artinya kesempatan atau kemungkinan terjadinya besar,sebaliknya peluang kecil artinya kesempatan terjadinya kecil.
Probabilitas suatu kejadian yaitu angka yang mengatakan kemungkinan terjadinya suatu kejadian. Nilainya di antara 0 dan 1. Kejadian yang mempunyai nilai probabilitas 1 yaitu tragedi yang niscaya terjadi atau sesuatu yang telah terjadi.Misalnya matahari yang masih terbit di timur hingga sekarang. Sedangkan suatu tragedi yang mempunyai nilai probabilitas 0 yaitu tragedi yang tidak mungkin atau tidak mungkin terjadi. Misalnya seekor kambing melahirkan seekor sapi.
Pada percobaan pelemparan sebuah dadu, ruang sampelnya yaitu S = {1, 2, 3, 4, 5, 6}, sedangkan titik-titik sampel percobaan tersebut yaitu 1, 2, 3, 4, 5, 6. Adapun sebarang himpunan penggalan dari ruang sampel disebut kejadian, biasanya dilambangkan dengan K. Misalnya, K = {2, 4, 6} yaitu tragedi munculnya muka dadu bertitik genap dengan n(K) = 3.
Perhitungan Peluang Suatu Kejadian dengan Frekuensi Relatif
Frekuensi relatif yaitu perbandingan banyaknya tragedi yang diamati dengan banyaknya percobaan.Frekuensi relatif dinyatakan dengan rumus sebagai berikut.
Ambillah sekeping uang logam, lalu lemparkan sebanyak 30 kali. Misalkan, hasil yang diperoleh yaitu muncul sisi gambar sebanyak 13 kali. Perbandingan banyak tragedi muncul sisi gambar dengan banyak pelemparan yaitu 13/30. Nilai inilah yang disebut frekuensi relatif.
Contoh Soal Frekuensi Relatif
Rino melempar dadu sebanyak 200 kali. Hasilnya yaitu muncul muka dadu sebagai berikut.a. Bertitik 1 sebanyak 25 kali.
b. Bertitik 3 sebanyak 17 kali.
c. Bertitik 6 sebanyak 56 kali.
Tentukan frekuensi relatif tragedi munculnya mata dadu bertitik 1, 3, dan 6.
Jawab:
Banyaknya percobaan yaitu 200
a. Kejadian munculnya muka dadu bertitik 1 sebanyak 25 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 1 yaitu 0,125.
b. Kejadian munculnya muka dadu bertitik 3 sebanyak 17 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 3 yaitu 0,085.
c. Kejadian munculnya muka dadu bertitik 6 sebanyak 56 kali.
Jadi, frekuensi relatif munculnya muka dadu bertitik 6 yaitu 0,28.
Perhitungan Peluang Suatu Kejadian dengan Rumus Peluang
Perhatikan kembali percobaan pelemparan sebuah dadu. Ruang sampelnya yaitu S = {1, 2, 3, 4, 5, 6} sehingga n (S) = 6. Misalkan, tragedi munculnya muka dadu yang bertitik prima dinyatakan dengan K = {2, 3, 5} sehingga n(K) = 3.Peluang munculnya setiap titik sampel di dalam ruang sampel yaitu sama, yaitu 1/6. Jadi, peluang munculnya muka dadu bertitik prima adalah
Selain dengan cara tersebut, nilai P(K) juga sanggup ditentukan dengan cara sebagai berikut.
S = {1, 2, 3, 4, 5, 6} maka n(S) = 6.
K = {2, 3, 5} maka n(K) = 3.
Uraian tersebut menjelaskan bahwa bila setiap titik sampel anggota ruang sampel S mempunyai peluang yang sama maka peluang tragedi K yang mempunyai anggota sebanyak n(K) dinyatakan sebagai berikut.
Contoh Soal Peluang
Siti melemparkan sebuah dadu. Tentukanlah peluang munculnya mata dadua. bertitik 3,
b. bertitik lebih dari tiga,
c. bertitik 1, 2, 3, 4, 5, 6,
d. bertitik lebih dari 6.
Jawab:
Oleh alasannya ruang sampelnya yaitu S = {1, 2, 3, 4, 5, 6} maka n(S) = 6.
a. Misalkan, A yaitu himpunan tragedi munculnya dadu bertitik 3 maka A = {3} sehingga n(A) = 1.
b. Misalkan, B yaitu himpunan tragedi munculnya dadu bertitik lebih dari 3 maka B = {4, 5, 6} sehingga n(B) = 3.
c. Misalkan, C yaitu himpunan tragedi munculnya mata dadu bertitik 1, 2, 3, 4, 5 dan 6 maka C = {1, 2, 3, 4, 5, 6} sehingga n(C) = 6.
Jadi, peluang munculnya mata dadu bertitik 1, 2, 3, 4, 5 dan 6 yaitu 1.
d. Misalkan, D yaitu himpunan tragedi munculnya mata dadu bertitik lebih dari 6 maka D = { } sehingga n(D) = 0.
Jadi, peluang munculnya mata dadu bertitik lebih dari 6 yaitu 0.
Baca juga: Ruang Sampel Suatu Percobaan
Sumber https://www.berpendidikan.com
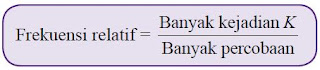




Post a Comment for "Pengertian Peluang Suatu Kejadian, Frekuensi Relatif, Rumus Dan Pola Soal Peluang (Probabilitas)"